NOTE: “Pulpo” is the Spanish word for “octopus”.
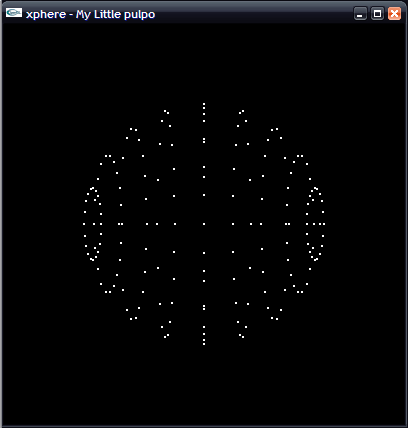
First of all, we need to create a sphere:
glBegin (GL_POINTS);
for (alpha=-PI/2; alpha<PI/2; alpha+=alpha_inc)
{
for (theta=0; theta<2*PI; theta+=theta_inc)
{
x = size*cos(alpha)*sin(theta);
y = size*cos(alpha)*cos(theta);
z = size*sin(alpha);
glVertex3f(x,y,z);
}
}
glEnd();
It’s the standard way to draw the vertex of a sphere, “size” represents the radius of the sphere… if you need more info, I recommend you to spend some time at Paul Bourke site.
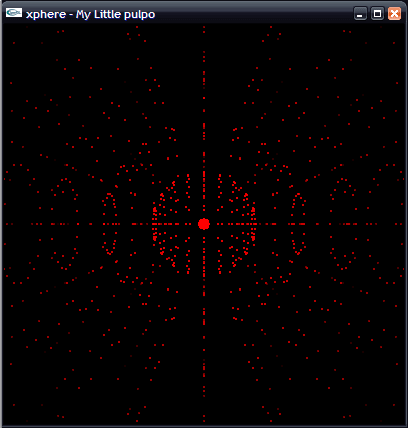
Ok, so the theory is to draw more spheres over this one, with incremental sizes… lets see an image…
It’s quite easy, you only need to increment the “size” value at each sphere. Now, the theory is to rotate only one of the sphere (the sphere of the center), and then, our program should automatically rotate all the surrounding spheres smoothly. C’mon! you almost got it!!!One of the problems is to implement our rotation routine, in order to draw the different points rotated, and some OpenGL functions like glRotatef, does not fit well for this, because we need to push and pop the matrix for each vertex… and that’s too much code & lot of wasted process time… simply sucks!!
The rotate routines are:
/////////////////////////////////////// // Process vertex rotations // X rot ny = (cos(xrot) * y) - (sin(xrot) * z); nz = (sin(xrot) * y) + (cos(xrot) * z); y = ny; z = nz; // Y rot nx = (cos(yrot) * x) + (sin(yrot) * z); nz = (cos(yrot) * z) - (sin(yrot) * x); x = nx; z = nz; // Z rot nx = (cos(zrot) * x) - (sin(zrot) * y); ny = (sin(zrot) * x) + (cos(zrot) * y); x = nx; y = ny;
nx, ny and nz are temporal variables. With this little routine, we can rotate a vertex (x,y,z), with the angles xrot, yrot and zrot (in radians, not degrees!!). So, we have some spheres, we have a rotation routine… we only need to rotate the spheres, but each one with the rotation angle increased respect the last one… for example, we rotate the smallest sphere 10º around the X axis, so, the Sphere 1 (the next one), should rotate 12º (10+2) around the X axis, and the second Sphere should rotate 14º (12+2), and go on!
This incremental value (2) can be decided by the user, spend some time to test some values and decide your favourite one :).… and… that’s it!! If you have understood all this crap, you should be able to understand this code:
void DrawPulpo(int mag, float xrot, float yrot, float zrot)
{
glColor4f(1,1,1,1);
float x,y,z;
float nx=0,ny=0,nz=0; // New point values (after angle tarnsform)
float dx,dy,dz;// Diferencial de la rotació (el que ens hem mogut respecte abans)
dx = (xrot - old_xrot) * mag;
dy = (yrot - old_yrot) * mag;
dz = (zrot - old_zrot) * mag;
old_xrot = xrot;
old_yrot = yrot;
old_zrot = zrot;
glBegin (GL_POINTS);
for (size=1; size<MAX_SIZE; size+=size_inc)
{
for (alpha=-PI/2; alpha<PI/2; alpha+=alpha_inc)
{
for (theta=0; theta<2*PI; theta+=theta_inc)
{
glColor4f(1,0,0,1-size/MAX_SIZE);
x = size*cos(alpha)*sin(theta);
y = size*cos(alpha)*cos(theta);
z = size*sin(alpha);
///////////////////////////////////////
// Process vertex rotations
// X rot
ny = (cos(xrot) * y) - (sin(xrot) * z);
nz = (sin(xrot) * y) + (cos(xrot) * z);
y = ny;
z = nz;
// Y rot
nx = (cos(yrot) * x) + (sin(yrot) * z);
nz = (cos(yrot) * z) - (sin(yrot) * x);
x = nx;
z = nz;
// Z rot
nx = (cos(zrot) * x) - (sin(zrot) * y);
ny = (sin(zrot) * x) + (cos(zrot) * y);
x = nx;
y = ny;
///////////////////////////////////////
glVertex3f(x,y,z);
}
}
xrot -= dx; // Calcule next rotation angles...
yrot -= dy;
zrot -= dz;
}
glEnd();
}
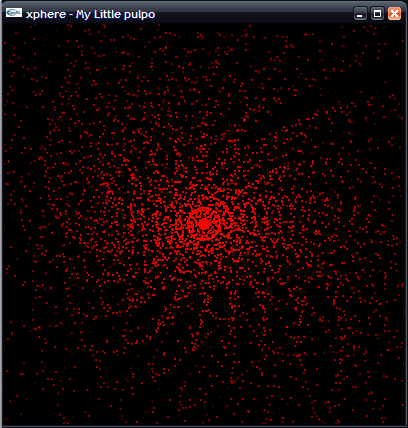
The theory is quite simple: draw spheres (MAX_SIZE defines the maximum number of spheres to draw), and each time we draw a new sphere, we increment the angle between them.
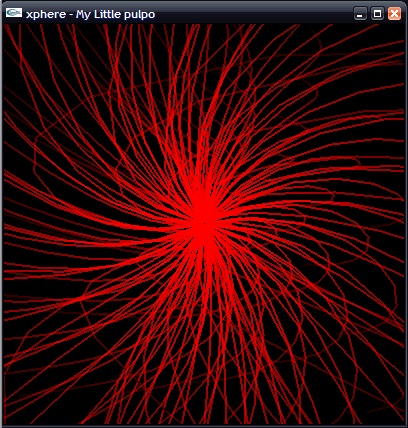
And, if we want to draw some lines… we have to modify some lines of code…
void DrawPulpo(int mag, float xrot, float yrot, float zrot)
{
glColor4f(1,1,1,1);
float x,y,z;
float nx=0,ny=0,nz=0; // New point values (after angle tarnsform)
float dx,dy,dz;// Diferencial de la rotació (el que ens hem mogut respecte abans)
dx = (xrot - old_xrot) * mag;
dy = (yrot - old_yrot) * mag;
dz = (zrot - old_zrot) * mag;
old_xrot = xrot;
old_yrot = yrot;
old_zrot = zrot;
for (alpha=-PI/2; alpha<PI/2; alpha+=alpha_inc)
{
for (theta=0; theta<2*PI; theta+=theta_inc)
{
// Restore rotation angles
xrot = old_xrot;
yrot = old_yrot;
zrot = old_zrot;
glBegin (GL_LINE_STRIP);//POINTS);
for (size=1; size<MAX_SIZE; size+=size_inc)
{
glColor4f(1,0,0,1-size/MAX_SIZE);
x = size*cos(alpha)*sin(theta);
y = size*cos(alpha)*cos(theta);
z = size*sin(alpha);
///////////////////////////////////////
// Process vertex rotations
// X rot
ny = (cos(xrot) * y) - (sin(xrot) * z);
nz = (sin(xrot) * y) + (cos(xrot) * z);
y = ny;
z = nz;
// Y rot
nx = (cos(yrot) * x) + (sin(yrot) * z);
nz = (cos(yrot) * z) - (sin(yrot) * x);
x = nx;
z = nz;
// Z rot
nx = (cos(zrot) * x) - (sin(zrot) * y);
ny = (sin(zrot) * x) + (cos(zrot) * y);
x = nx;
y = ny;
///////////////////////////////////////
glVertex3f(x,y,z);
xrot -= dx; // Calcule next rotation angles...
yrot -= dy;
zrot -= dz;
}
glEnd();
}
}
}
Some definition of the used variables:
- Mag: here we control the rotation increase among the spheres
- Xrot,.. zrot: Here we decide how many degrees we want to rotate the first sphere
- Old_xrot,.. old_zrot: Here we store temporary values of the old rotation angles, each
- Dx,.. dz: variable to store the angle increment
And… that’s it!!!! HAPPY CODING!!!!
… Now the homework!! 😉
- Optimize the drawing function (can be optimized a LOT!).
- Move our pulpo!! here we only can rotate it, and he wants to move around the screen!!
- Make our pulpo solid… he told me that he does not like very much the lines!!
- Make your demo!! c’mon! people is waiting!!
- ….